Boost Factors¶
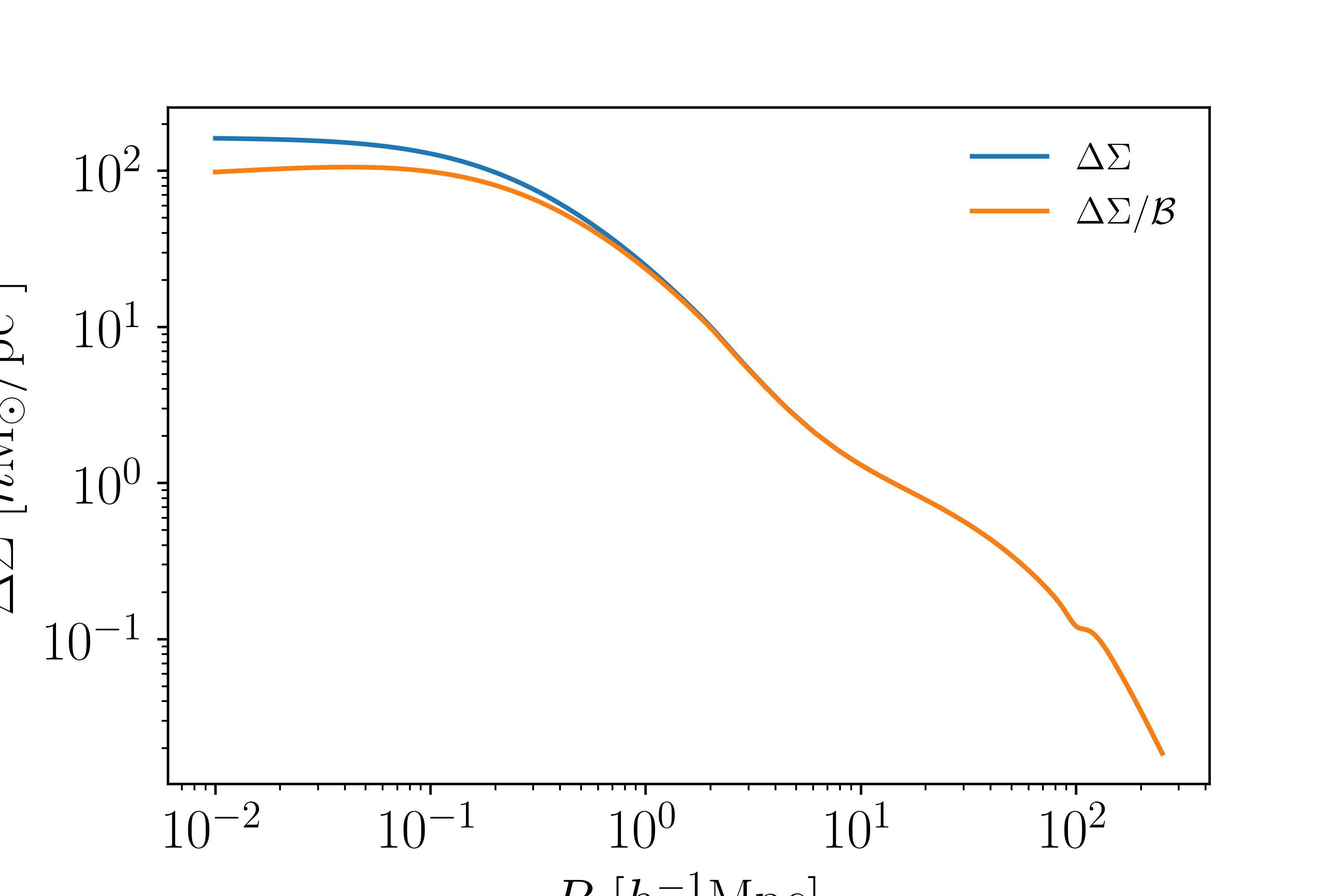
In galaxy cluster weak lensing, a significant systematic issue is cluster member dilution also known as boost factors. The idea is that if some cluster galaxies are misidentified as source (background) galaxies, then your weak lensing signal is diluted due to the fact that the cluster member galaxy won’t be sheared or magnified. Traditionally, one calculates or estimates this correction and “boosts” the data vector. This boost factor is radially dependent, since you will tend to misidentify cluster members close to the cluster more than those farther out. Mathematically this looks like
where \(f_{\rm cl}\) is the fraction of cluster members misidentified as being source galaxies. For shorthand, we write \(\mathcal{B} = (1-f_{\rm cl})^{-1}\). This module provides multiple models for \(\mathcal{B}\).
NFW Boost Model¶
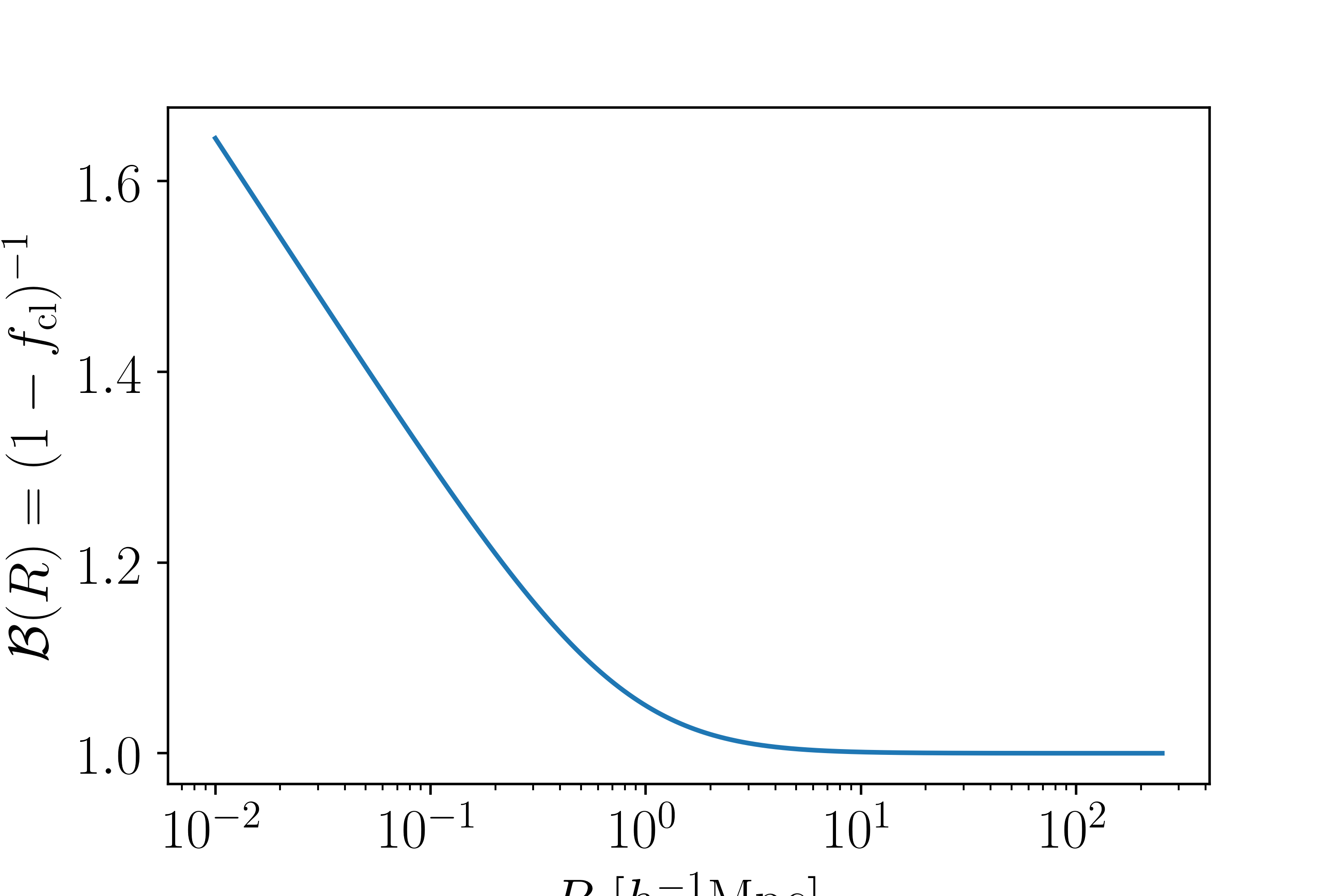
In McClintock et al. (in prep.) we model the boost factor with an NFW model:
where \(x=R/R_s\) and
Parameters that need to be specified by the user are \(B_0\) and the scale radius \(R_s\). To use this, you would do:
from cluster_toolkit import boostfactors
import numpy as np
R = np.logspace(-2, 3, 100) #Mpc/h comoving
B0 = 0.1 #Typical value
Rs = 1.0 #Mpc/h comoving; typical value
B = boostfactors.boost_nfw_at_R(R, B0, Rs)
Powerlaw Boost Model¶
In Melchior et al. we used a power law for the boost factor.
Here, the input parameters are \(B_0\), the scale radius \(R_s\), and the exponent \(\alpha\). This is also available in this module:
from cluster_toolkit import boostfactors
import numpy as np
R = np.logspace(-2, 3, 100) #Mpc/h comoving
B0 = 0.1 #Typical value
Rs = 1.0 #Mpc/h comoving; typical value
alpha = -1.0 #arbitrary
B = boostfactors.boost_powerlaw_at_R(R, B0, Rs, alpha)
This figure shows the NFW boost factor model:
This figure shows how the boost factor changes the \(\Delta\Sigma(R)\) profile: